
Scrutinizing Stock Prices in Eye of Benford’s Law Using Python

The Law
One and half decade back while I was pursuing my Chartered Accountancy, I had come across interesting topic on fraud detection in accounting and taxation, using Benford’s Law. Benford’s Law is nothing complex, it just states that unless any data is manipulated, the occurrence of first digit of naturally occurring numbers follows a pattern and shows consistent probability of occurrence. This is because of simple logic that the first digit if it is 1 must increase by 100 percent to change to 2 while for 2 to change to 3, it only needs to increase by 50 percent. Newcomb first noticed and Frank Benford rediscovered this occurrence of logarithmically decaying distribution of first digit from 1 to 9 represented by the formula.
P(D1=d) = log10(1 + 1/d) (Where d is the number from 1 to 9)
Being in a role of Investment Banker at present, I wondered whether the often controversy of anomalies in the trading of stock in market could be scrutinized using same law. While there seemed difficulty as for Benford’s Law to hold true, there needs to be large sample size, but manipulations or malpractices in any trading stock happens for a short period. However, few have tried to scrutinize the rampant trading manipulations of cryptos like Bitcoin. This law however has been effectively used in fraud detection in accountancy, taxation, elections etc.
Dataset
For veracity of whether the Benford’s Law applies truly, I took the NEPSE Closing prices from the inception. Further data of closing prices of two highly volatile scrips from Finance Companies Sector was taken for testing purpose.
Python Codes
Step 1-Import necessary Python Libraries and Defining Benford’s Percentages
#Importing required Libraries
import numpy as np
import pandas as pd
import collections
import matplotlib.pyplot as plt
#Probabilities as per Benford’s Law
benfords_prob = [30.1, 17.6, 12.5, 9.7, 7.9, 6.7, 5.8, 5.1, 4.6]
Step 2-Import NEPSE Closing Indexes and Sample Finance Company Prices
#Reading closing index of NEPSE
NEPSE_data = pd.read_csv("NEPSE.csv")
NEPSE_close=NEPSE_data["Close"]
#Reading prices of sample Finance Company No. 1
F01_data = pd.read_csv("F01.csv")
F01_data.columns = "Date","Prices"
F01_prices=F01_data["Prices"]
#Reading prices of sample Finance Company No. 1
F02_data = pd.read_csv("F02.csv")
F02_data.columns = "Date","Prices"
F02_prices=F02_data["Prices"]
Step 3-Creating Function for the purpose of calculating percentage
#Function to calculate percentage of first digit occurrences
def calc_percentage(data):
first_digit_percentage = [] #Defining List to accumulate values
first_digits = list(map(lambda n: str(n)[0], data))
first_digit_frequencies = collections.Counter(first_digits)
for n in range(1, 10):
data_frequency = first_digit_frequencies [str(n)]
data_frequency_percent = (data_frequency / len(data))*100
first_digit_percentage.append(data_frequency_percent)
return (first_digit_percentage)
Outcomes (Visualization)
Step-4 Plotting and Visualizing the Graphs
#Calculating first digit of NEPSE closing prices and plotting using Matplotlib alongside Benford’s line
x=np.arange(1,10)
y=calc_percentage(NEPSE_close)
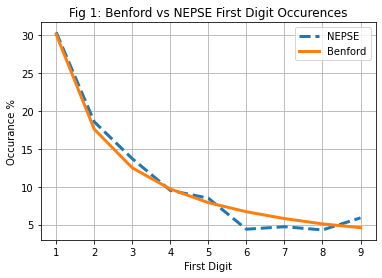
plt.title("Fig 1: Benford vs NEPSE First Digit Occurences")
plt.xlabel("First Digit")
plt.ylabel("Occurance %")
plt.plot(x,y,label='NEPSE',linewidth=3,linestyle="dashed")
plt.plot(x,benfords_prob,label='Benford',linewidth=3,linestyle="solid")
plt.grid()
plt.legend()
#Calculating first digit of Sample Finance Co # 1 Prices and plotting using Matplotlib alongside Benford’s line
x=np.arange(1,10)
y=calc_percentage(F01_prices)
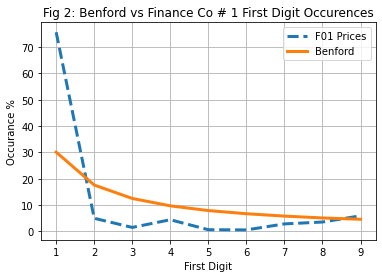
plt.title("Fig 2: Benford vs Finance Co # 1 First Digit Occurrences")
plt.xlabel("First Digit")
plt.ylabel("Occurance %")
plt.plot(x,y,label='F01 Prices',linewidth=3,linestyle="dashed")
plt.plot(x,benfords_prob,label='Benford',linewidth=3,linestyle="solid")
plt.grid()
plt.legend()
#Calculating first digit of Sample Finance Co # 2 Prices and plotting using Matplotlib alongside Benford's line
x=np.arange(1,10)
y=calc_percentage(F02_prices)
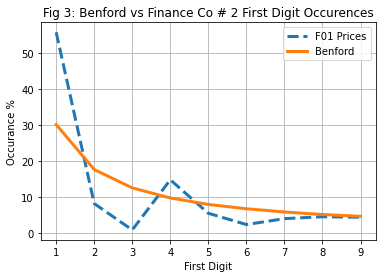
plt.title("Fig 3: Benford vs Finance Co # 2 First Digit Occurrences")
plt.xlabel("First Digit")
plt.ylabel("Occurance %")
plt.plot(x,y,label='F01 Prices',linewidth=3,linestyle="dashed")
plt.plot(x,benfords_prob,label='Benford',linewidth=3,linestyle="solid")
plt.grid()
plt.legend()
Conclusions:
While as initially disclaimed, Benford’s law can not be litmus test for finding manipulations, but given that there is adequately large data, the prescribed probability distribution of Benford’s Law should certainly hold true if it is naturally occurring data. In Figure No. 1 when NEPSE Closing Indexes are plotted over Benford’s distribution, the plots seem to be nearly overlapping each other except at digit 6 and 7. Indexes which are mix of large number of various scrips can hardly be manipulated in huge amount and hence seems to follow the Law. In case of sample Finance Companies which had largely volatile price movements in recent periods, the plot seemed hugely deviating from the Law specially where the first digit is 1 (so possibly somebody wanted to keep prices above 1000 😉)
CA. Dinesh Thakali (Author is employee of Prabhu Bank Ltd and currently Managing Director at Prabhu Capital Ltd. Views expressed are personal and Author intends only to illustrate the results of Law but doesn’t prescribes or authenticates usage of the methods for any purpose) —Published in ShareSansar.com — 2022-April-18

लकडाउन, वर्क फ्रम होम, युरोप र हाम्रो नेपाल
"तुफानलाई शान्त बनाउन सकिँदैन, आफू शान्त रहने र सो टर्ने पर्खाइ बाहेक अन्य समाधान रहँदैन "
सन् २००६ तीर फाइनान्सियल टाइम्सका स्तम्भकार लुसी केलेवेले वर्क फ्रमहोम बारेमा लेखेको कोलमको बाक्य हो यो ।
कोरोनाविरुद्ध लकडाउनमा घरमै सेल्फ आइसोलेशन बसेर कार्यस्थलसँग विधुतिय सम्पर्कमा रहनु पर्दा लुसीको उक्त भनाइको याद आयो । जुन अहिले खोज्दा भेटिँन ।
यस्तै म्यानेजमेन्ट ट्रेन्ड र जार्गोन बारेमा स्याटेरिकल कोलम लेख्ने उनको त्यो लेख बल्ल अनुभुत भइरहेको छ । सो समयमा भर्खर वर्क फ्रम होम ९टेलि कम्युटिङ्ग०, फ्लेक्जिवल वर्किङ्ग आवरजस्ता कन्सेप्ट शुरु भएकोमा सो कति प्रोडक्टिभ र कति फाइदाजनक वा बेफाइदाजनक भन्ने सटिक विश्लेषण थियो ।
घोडाको नालले किल्चिएर टुँडी नामको प्रेत मारिएकोले उत्सव मनाउन शुरु भएको घोडे जात्राकै दिन कारोनाको भाइरस फैलन नदिन नेपाल सरकारले लकडाउन गर्यो । लकडाउनपछि व्हाट्सएप, जुम, भाइवर अनि ल्यापटप नै हामी सबैको कार्यस्थल हुनथाल्यो ।
लकडाउनपछि माइक्रोसफ्ट टिम्स, स्ल्याकमा दसौं लाख थप युजर थप भए । जुम, व्हट्सएपमा ४० प्रतिशतसम्मको प्रयोग बढेको सन्दर्भमा वर्क फ्रम होम संसार जगतमा सान्दर्भिक र एकमात्र उपाय हुन गएको देखियो ।
लुसीले सो लेख लेख्दा आफैं केही समय घरबाट काम गरेर अनुभव लिएकी थिइन् । उनले लेखेकी थिइन, ‘छिनछिनमा कफी खान उठ्न मन लाग्ने, त्यसै लघुशंका लागेजस्तो हुने आदिले कन्सन्ट्रेसन रहेन ।’
लकडाउनपछि सामाजिक सञ्जालभरी पुरानो जमानाको फोटोको उत्खननको खेती मौलायो । र, त्यसमा मुनामदनलाई माथ दिने कमेन्टहरु अनि उक्त कमेन्टमा फर्काइने साहित्यिक जवाफ । सामाजिक सञ्जालमा भाइरल बनेका टोलहरु । यो देख्दा हामी नेपालीहरु निकै क्रिएटिभ भएको अनुभूति पनि मिल्यो ।
दैनिक मिष्ठान्न पकवानको तस्विर देख्दा कसैको कार्यस्थलप्रति त्यति कन्सन्ट्रेसन रहेजस्तो लागेन अहिले पनि । लकडाउन सकिँदासम्म ज्यानको तौल एकदुई किलो थप हुँदा सामान्य नै लिए भयो ।
लकडाउनमा बल्ल थाहा भयो । मान्छेहरुले सधैं फलाने व्याङ्कवेट कहाँ हो भनेर सोध्न आएको त घर मुन्तिरको बाटैमा रहेछ । पल्लो पट्टीको चोककोे नाम भानु चोक रहेछ । बुढानिलकण्ठ मन्दिरमाथि शिवपुरी, स्तुपादेखि नारायण गोपाल चोकसम्मको ३६० डिग्री भ्यू पनि घरकै छतबाट उपलव्ध रहेछ ।
एकजना बहिनी कहिले कम्पाउण्डमा जगिङ्ग, कहिले चिया पकाउने विधिबारेमा लाइभ दिइराखेकी थिइन् । डेढ घण्टाको नेटफ्लिक्सको मुभि छोटो भएर सबैजना सिरिजतिर लागेर सम्पूर्ण सिजन नै सकाएको देखियो ।
पढ्दाताका हामी केही साथीहरु रिडर्स क्लब नै बनाएर अहिले बच्चाहरुको डे होस्टल भनेजस्तै बिहानदेखि बेलुकासम्म बसी पढ्ने जमर्को गर्थ्यौं । खाजा र लन्च पोको पारेर क्लवमा छिर्ने हामी पालैपालो सबको टिफिन खाँदा पनि डिनरसमेत ब्रेक फास्टकै समयमा सकिने अवस्था आएपछि हामी तितरबितर हुन्थ्यौं । अहिले वर्क फ्रम होम पनि खाली खानाबाहेक अरु कसैलाई केही सम्झना भएजस्तो लागेन ।
लुसीले थप लेखेकी थिइन्, ‘एक हप्ताको बसाइमा पल्लो घरका कुकुरको रङ्ग कस्तो रहेछ रु कति मान्छे बस्दा रहेछन् रु सम्पूर्ण जानकारी भयो ।
लकडाउनमा बल्ल थाहा भयो । मान्छेहरुले सधैं फलाने व्याङ्कवेट कहाँ हो भनेर सोध्न आएको त घर मुन्तिरको बाटैमा रहेछ । पल्लो पट्टीको चोककोे नाम भानु चोक रहेछ । बुढानिलकण्ठ मन्दिरमाथि शिवपुरी, स्तुपादेखि नारायण गोपाल चोकसम्मको ३६० डिग्री भ्यू पनि घरकै छतबाट उपलव्ध रहेछ । घरमा कहाँ झार पलाएछ रु कहाँ पर्खाल चिरा पर्न आँटेछदेखि कति क्षेत्रफल दुबो सुक्न थालेछ रु भन्नेसम्मको इन्स्पेक्सन भयो ।
लुसीले अर्को प्यारामा लेखेकी थिइन्( ‘को वर्कर नजिक नभएको आभाष भएपछि छिनछिनमा इमेलबाट हेल्लो भन्न मन लाग्ने । र, अफिसमा बसेकाले पनि मेसेज पठाइरहने रहेछन् । लकडाउनले थाहा भयो, ह्वाट्सएप, भाइवर, जुममा विभिन्न विभाग, क्षेत्रगत र सम्पर्कमञ्च गरी दर्जन ग्रुप रहेकोमा सोमा छिनछिनमा बज भइने रहेछ ।’
अफिसमा निश्चित समयमा सम्पर्क भइनेमा, विधुतिय हुँदा बिहानदेखि रातिसम्म आआफ्नो सहजता र आवश्यकतामा बज गरिदिने हुँदा वर्क फ्रम होम होइन ‘वर्क अल डे लङ्ग’ भनेजस्तो अनुभूत रहने रहेछ । एक जनाले पठाएको म्यासेज सान्दर्भिक नभएता पनि सबै ग्रुपमा जाँदा छिनछिनमा अनावश्यक पोक भइने रहेछ बेफ्वाकमा ।
लुसीले फेरी सबै नेगेटिभमात्र भनिन् भन्ने भ्रम नरहोस् । उनले लेखेकी थिईन्, ‘डेढ घण्टाको पट्यार लाग्दो आवतजावतको समय कम भएको महशुस भयो ।’
पक्कै पनि कोटेश्वर, कलंकी, महाराजगञ्ज, थापाथलीको बस्नु पर्ने जामको पिडा हामीले यो ८ दिनमा विर्सन थालेका छौ । पास लिएर लिन आएका ड्राइभर भाईले भन्दै थिए, ‘दुबईमा मल्टी लेनमा चलाएको जस्तो भयो सर ।’ स्याटलाइट तस्विरमा प्रदुषणको मापनमा अस्ट्रेलियाको आगलागीले क्षतविक्षत ओजोन तह पुनरागमन भएको देखाएको छ । अर्को फाइदा सो पनि होला घरमै कार्यस्थल बनाउँदा ।
अस्ति एउटा भाईले भन्यो ( इटालीमा त नोभेम्वरमा नै थियो रे कोरोना ।’ नोभेम्बरमा नै एकहप्ता युरोपका ५ देश म्याराथन भ्रमण गरेर आएको मेरो घाँटी खसखस भए जस्तो भयो ती भाइको कुरा सुनेपछि । जर्मनीबाट आम्सटर्डम प्रवेश हुँदा रविन्द्र मानदाइले बाटोमा लहरै भएका घर देखाउँदै भन्नुभयो, ओपन विन्डो हुन्छ याहाँ ज्यादा तर । पारदर्शिता र खुलापनको आभाष दिनहोला धेरै घरमा पर्दा रहेनछ । ठुला ठुला अफिस घर पनि बाहिरबाट पारदर्शीरुपमा देखिने । त्यही खुलापनकोे असरले होला अहिले युरोपमा कोरोना संक्रमितको ग्राफ सगरमाथा चढेजस्तो बढिरहेको छ ।
आम्सटर्डममै बस्ने साथीले विवरण प्रदान गरे, आम्सटर्डम पुरानै आर्किटेक्चरमा विस्तारित छ । तर दोस्रो विश्वयुद्धमा पूर्णध्वस्त भएको रोटर ड्रम आधुनिक वास्तुकलाले पुनःनिर्मित भएको हो । सो भनाइ सम्झिँंदा अहिलेको मन्दी र आर्थिक संकटउन्मुख विश्व अर्थतन्त्रले चिन्तित मानसपटललाई केही ढाडस भयो ।
७० देखि ८५ मिलियनको ज्यान लिएको दोस्रो विश्वयुद्धबाट त शहरहरु पुननिर्मित हुने रहेछ, अझ मजबुत र आधुनिक भई, यो समय पनि कसो नटर्ला र ।
(मिति २०२० अप्रिल ११ मा क्लीकमाण्डु डट कममा प्रकाशित)

Towards premature maturity
As a student, I was an ardent fan of Financial Times columnist Lucy Kellaway, who wrote a regular column on modern corporate culture. A successful writer, she suddenly interrupted her regular profession to start teaching and establishing Now Teach, a forum to take onboard other successful professionals to take a break and start teaching.
On July 13, 2018, she admitted that though her change of the regular profession had many hiccups, the foremost being her slashed income by 80 per cent, she said it was wonderful to start all over again and that there seemed a lot of people out there who felt the same way.
One revered musician in his 90’s said in an interview, “Life goes like a lightening, I just feel like I blinked my eyes, and 90 years have passed already.” I had a similar feeling the other day when I sat with my college friend for lunch. It seemed like yesterday that we were together jogging or scoring baskets in the basketball court or going up and down the hills of Nainital. Alas, that was 20 years ago. I realized that we had been running with life so hard that we seem to have missed what we went through in between.
Modern life has become such that we are running on an inescapable treadmill of time. Only its ambience changes to give us the different flavors of life, like graduation, jobs, marriage, children and promotions.
The realization that life’s too short for worries and stress is coming faster to the new generation. Every now and then we hear them say, “Why worry so much? What’s in life?” Amazingly that was what we used to hear from our grandparents in our childhood. Come holidays and there are flocks of people now trying to go out on a vacation, even to destinations abroad.
The determination to lead a quality life has got diminished by being confined to the mundane routine life. We are being time and again misled into believing that happiness means money, jobs, promotion and respect. Many banker friends, who are well revered in their profession, want to leave the job the very next day as they feel suffocated.
Recently I met a senior banker, who pointed to packed personal stuffs, ready to move out at any instance. A cousin sister of mine, who recently left a good bank job, said about her new life, “To be frank, I’m enjoying this phase, I loved my work, but I was not happy with the everyday routine”.
Indeed, we seem to be moving towards premature maturity, perhaps for good.
(Published in The Himalayan Times on 2019 October 13)

दोबाटोमा तिब्बत
त्रिभुवन विमानस्थलको प्रस्थानद्धारमा हग गर्दै दिदीले भनिन् आमा घुम्नु भयो अव बुवालाई पठा एक पटक यु.के. डुल्नलाई । घरमा बेलुकी सन्देश प्रवाह गरे बुवालाई । जादिन यु.के., बरु तिब्बत लगिदे एकपटक, अनौठो तर मलाई नि मन पर्ने माग आयो । त्यो मिस्टिकल म्याजिकल ल्हासा मेरो पनि चेकलिस्टमा प्लेसेस टु गो लिस्टमा थियो । दुई चार साथीभाईलाई सोधे कसरी जान सकिन्छ । केही पत्तो लागेन । सामाजिक संजालको प्रयोग गरे, फेसबुक पोस्टमा दिदी सोविताको रिप्लाई आयो हाम्रो रोयल माउन्टेन बिर्सेको ? तिब्बत पर्मिटको प्राप्ति पछि चिनको गु्रप भिसाको लागि आवेदन गरियो । एयर चाइनाको विमानद्धारा डेढ घण्टाको उडानद्धारा ३,५०० मिटरमा अवस्थित विश्वकै १३ औं अग्लो ल्हासाको गोङ्गर विमानस्थलमा उत्साहका साथ अवतरण गर्यौ । आकाशमा हिमाल नै हिमाल माथि उडिरहँदा बुवाले समय समयमा भिडियो बना त भन्दै आफ्नो चिनमै निर्मित हुवावे फोन दिनु हुन्थ्यो । विहान मर्निङ्ग वाकमा जाँदा चिया साथिलाई तथा घरमा भेट्न आउने नातेदारलाई देखाउने मेसो ।
तिब्बतको राजनैतिक संवेदनशिलता, हाम्रो मंगोलियन अनुहार त्यो माथि मुस्ताङ्गको मूल, केही समस्या हुने हो कि भन्ने त्रासदी मनमै थियो । अध्यागमनमा त्यो सत्य निक्लियो । अमेरिका, जापान, युके मा भ्रमणको भिसा भएको मेरो नेपाली पासपोर्ट देख्ना साथै छेउको कुना कोठामा लगि हाले । भिजिटिङ्ग कार्ड खल्टिमै राखेको थिए यही प्रयोजनलाई, दिए । अरु पद र पढाई नजरअन्दाज गरेर एल.एल.वि. देखेसी ओह लयर भनेर छाडि दिए । संसार भर जस्तै वकिलको इज्जत यहाँ काम गर्यो, नेपालमा वकिलसावहरुको यत्ति इज्जत होला त, मनमनै गमे ।
अध्यागमनकै एक महिला प्रहरीले नमस्ते तिब्बतमा स्वागत छ, एकछिन बस्नुस् तपाईको गाइड आएर लैजान्छ भनिन्, नेपालीमा नै फरर । भर्खर अध्यागमनमा केरकारमा परिएका बुवा झन्दै ढल्नु भएन चिनिया टोनमा नेपाली सुनेर । बुझ्दै जादा पछि थाहा भयो, तातोपानी नाकामा बसेका चिनिया तथा तिव्बतीहरु मज्जाले नेपाली बोल्दा रहेछन् ।
गाईड केल्साङ्गले खादा लगाइदिदै गर्दा बुवाले सोध्नु भयो, ढ्होक्पा र्हे? अर्थात् तिबेतन हो ? ति गाईड नि कस्सो फेन्ट भएनन्, तिबेतन भाषा सुनेर । पोखरा पृथ्विचोकमा क्याम्प रहेकोले गुम्वा जाने बुवालाई केही भाषा ज्ञान भएकोमा मलाई चाही बुवा तिबेतन बोल्दा डिपोर्ट हुने हो की भन्ने डरले पिरोल्न थाल्यो । अझ केल्साङ्गले ब्रिफिङ्ग गरे, राजनैतिक कुरा नगर्नु, गाइड बिना गुम्वा वा दरवार नजानु, जहाँ तही फोटो नखिच्नु, सरकारी चिन्ह भएको बिल्डिङ्ग वरिपरि नबस्नु तथा दलाई लामाको कुरा नगर्नु । मनको उत्साहमा चिसो खनाईए झै भयो ।
उचाँईमा अचानक आगमन भएकोले एक दिन एक्लिमेटाईजेशनलाई बस्नु पर्ने आइटनरी रहेछ । बेलुकी बाबु छोरा हामी बसेको याक होटलबाट पश्चिम तर्फको चोक निर टहलियौ । साच्चै, चिसो स्वच्छ हावा, मनमोहक दृश्य, कलात्मक कुदिएका भवनहरु, मन आनन्दित भयो । झट्ट फोन निकाले, खिच्न मिल्ने हो कि होइन अन्यौल परे, जे परे पर्छ भनेर हिड्दा हिड्दै बुवाको फोटो र आफ्नो सेल्फी लिए, मन मनै समातिने त्रासका साथ ।
तिब्बतको आफ्नै भाषा, कला, सभ्यता तथा राजनैतिक धार्मिक इतिहास छ । तिबेतन राजाहरु मध्ये सातौं राजा स्रोङ्गचन गम्पोको धेरै योगदान देखिन्छ । १४ औं दलाई लामाले सन् १९५९ मा देश छाड्दा सम्म बसेका पोटाला दरवार लगायत सो अगाडी तिबेतको प्रशासनिक कार्यको प्रयोग भएको ड्रेपुङ्ग दरवार, नोर्बुलिङ्कका दरवार र सेरा गुम्वामा समेत उनै राजाको मूर्ति निकै महत्वका साथ राखिएको छ । सातौं शताब्दी तिर त्यस ताका नेपालका राजकुमारी भृकुटीलाई बिवाह गरेका राजा स्रोङ्गचन गम्पोले ज्होखाङ्ग गुम्बा बनाएको पाईन्छ । सन् १९६० ताका सांस्कृतिक क्रान्तिको मौकामा धेरै गुम्बा, धार्मिक किताव तथा मुर्तीहरु तोडफोड भएकोमा सो को अवशेषको रुपमा केही जलेको कालो काठहरु अहिले पनि सो गुम्बाको प्रबेशमा देखिन्छ । मानव समबेदनाले होला भने नेपाली चेलीको दरबार भनेसी अर्कै लाग्यो, पोटाला दरबार भन्दा ज्होखाङ्ग दरबार मलाई बढि आस्थावान लाग्यो । अन्य सबै गुम्बा तथा दरवारहरु तिब्बत चिसो स्थान भएकोले दक्षिण फर्केकोमा सो गुम्बा नेपाली संस्कृती अनुसार पूर्व फर्केको छ । सो मा नेपालबाट नै लगिएको मूर्ती फुटाइएकोमा पुनरुत्थान गरेर हाल उत्तरमा रहेको रामोच्छे गुम्बामा राखिएको छ ।
पोटाला दरवारमा छिरे पछि एक घण्टामा बाहिर निक्ली सक्नु पर्ने रहेछ । कारण, तिब्बत अटोनोमस क्षेत्रमा मात्र सन् २०१८ मा मात्र ३ करोड पर्यटकले भ्रमण गरे जसबाट पर्यटन क्षेत्रको मात्र आम्दानी ७.२ अर्व अमेरिकी डलर रह्यो । २०१९ मा सो संख्या ४ करोड पुग्ने अनुमान गरिएको छ । पोटालाको भिडलाई व्यवस्थापन गर्न सो समय तोकिएको रहेछ । चौथौं दिनमा ब्रम्हपुत्र किनार हुदै याम्द्रुक छो तालको भ्रमणमा निक्लिदा तिब्बतको त्यो धार्मिक राज्यमा भौतिक प्रगतीका लागि चिनले गरेको लगानीको स्पष्ट झलक देखियो । हिमाल नै रहेको करिव ४,६०० मिटरको उचाईमा समेत हाम्रो राजमार्ग भन्दा राम्रो पिच बाटो बनेको छ । दाँया बाँया हिमाल अनि बिचमा बाटो हुँदै गुड्दा प्रकृती र बिकासको उत्कृष्ठ सम्मीश्रणको महशुस भयो । गोङ्गर एयरपोर्टबाट निक्लेर ल््हासा सम्मको ६२ कि.मि. को यात्रामा नै दर्जन बढि टनेल बनेको पाईयो जसले हाम्रो देश पहाडले गर्दा पछाडी परेको रहेनछ भन्ने भान बनायो । सिचुवान–तिब्बत हाइवेमा नै ७ कि.मि. सम्मको टनेल ६,१६८ मिटरको उचाँइमा बनेको छ ।
अरु पद र पढाई नजरअन्दाज गरेर एल.एल.वि. देखेसी ओह लयर भनेर छाडि दिए । संसार भर जस्तै वकिलको इज्जत यहाँ काम गर्यो, नेपालमा वकिलसावहरुको यत्ति इज्जत होला त, मनमनै गमे ।

पोटाला दरबारबाट पूर्व तर्फको चोकमा के एफ सी मा टन्नै चिनिया तथा तिब्बेतनहरु खाई रहेको भेटियो । अलि तल बर्गर किङ्ग, पुमा, जिप, एडिडास लगायतका बिदेशी सपहरु थिए । त्यही माथि पोटाला दरबारमा छैठौं सातौं शताब्दीमा बनेका बिशालकाय स्वर्ण जडित हजारौं मूर्तीहरु, स्र्वण अक्षरमा लेखिएका धार्मिक आलेखहरु, ठूला ठूला लामाहरुको अस्तुहरु, कलात्मक मण्डलाहरु तथा बडेमानका स्तुपाहरु थिए । पुरानो मात्र होइन आगामी दिनमा पुनरागमन हुने मैत्रेय बुद्धको समेत मूर्ती कल्पित गरि राखिएको छ ।
ज्होखाङ्ग गुम्बाको वरिपरि बर्खोर बजार रहेको छ जुन यहाँको असन बजार जस्तै तिबेतनहरुको पारम्पारिक बजार रहेको छ । छुर्पी, चिया, चौंरीको घ्यू, याकको मासु, पारम्पारिक परिधानहरु, पारा (तिबेतनहरुले खेल्ने सामाग्री), खादा, धुप तथा पूजाका सामाग्रीहरु, भाडा कुडा एवं जडीबुडीहरु बेच्न राखिएको सो बजारको चोकमा पुरानो चलन अनुसारको सम्थिङ्ग व्यापारीहरुको गहनाको मार्केट पनि रहेछ । सो मार्केटमा उभिएरै व्यापार हुने, किन्ने र बेच्ने नबोली लामो कपडाको बाहुला भित्र हात छिराई भित्रनै इशाराको माध्यममा मूल्य छिन्ने रहेछ । सो क्षेत्र रैथाने तिब्बती बौद्धहरुको बाहुल्यता पाए, अन्यमा चिनिया हान समुदायले व्यापार ओगटेको देखिन्छ ।

यसरी मूल्यांकन गर्दा तिब्बतले बाटो, शिक्षा, पर्यटन, प्रविधी, हाइड्रो लगायतमा राम्रो प्रगती गरी आर्थिक सबलता तथा स्थायित्व तिर लम्केको देखिन्छ भने पोटाला दरबार तथा रैथाने तिब्बेतनहरुले आफ्नो धार्मिक राजनैतिक स्वतन्त्रताका साथै गुमाएका आस्थाका केन्द्र धर्मगुरु दलाई लामालाई मिस गरे जस्तो लाग्यो । तिब्बतमा पाइला टेके देखिनै वि च्याट, टिकटक लगायत चिनले प्रबद्र्धन गरेका बाहेक अन्य विधुतिय सामाग्री मेरो फोनमा चलेको थिएन । काठमाण्डौं भित्रनै पनि जुनसुकै नयाँ ठाँउमा जानु पर्दा गुगल म्याप चलाउनु पर्ने तथा जे पनि गुगल सर्च गर्ने बानी भएकोमा भ्रमणनै कस्तो तरकारीमा नुन नभएको तथा उकुस मुकुस युक्त जस्तो लाग्यो ।

नेपाल फर्किनेको अघिल्लो रात एक्लै राति पोटाला दरबारलाई फेद फेदै कोर (परिक्रमा) लगाए । रातमा उज्यालो धपक्क बलेको दरबार घुम्दै मनमनै सोचें पश्चिमाहरुले भने जस्तो धर्म र स्वतन्त्रताको पथ तिर लम्कन्छ होला तिब्बत् । फेरि सोचे, तिब्बतीहरुले अहिले स्वास्थ्यको कारणले खान छाडेको बटर टि (नुन चिया) जस्तै धर्म भन्दा बिकास तर्फनै लम्कन्छन कि आफ्नो सन्ततीको प्रगतीका लागि । कस्तो दोबाटोमा छ तिब्बत् ।
(मिति २०१९ मे ८ मा क्लीकमाण्डु डट कममा प्रकाशित लेख)

मर्दीको उकालो चढ्दा बैंक दिनेश थकालीलाई फुरेका पाँच व्यवस्थापकीय शूत्रहरु ।
गत साता प्रकृतिले सम्पूर्ण डाँडा सेताम्मे हुने गरि खुला दिलले दिएको पूर्ण हिमपातले जुम्ला र मुस्ताङ्गका स्याउ बारीलाई झै मेरो स्मृती पटलमा केही अघि म र मेरी जिवनसंगिनीले गरेको मर्दी भ्रमणको स्मरणले सिंचित गरिदियो । हामी आज जे छौ, त्यो हरेक अन्य मानिससँगको अन्तरक्रिया, विभिन्न आरोह अवरोहको अनुभवको संगालो, समय तथा वातावरणसँगको घर्षणले खारिएर बनेको भन्ने मेरो मान्यता हो । यस भ्रमणले पनि केही मात्रामा व्यवस्थापनका मिहिन तर महत्वपूर्ण सुत्रहरु पुनराबृत्ति गरि मनन गर्न सहयोग गरेको छ ।
लिनियर प्रक्षेपण भ्रामिक हुन सक्छ: एकाविहानै पोखराबाट ट्याक्सीमा फेदि हुदैं धम्पुस पुगियो । हेम्जामा फिर्के खोला दाहिने हुदैं फेदी सम्म लगभग समथरमा गुडेका हामी त्यसपछि धम्पुसको उकाली चढ्न मारुतीलाई हम्मे हम्मे भयो । धम्पुस देखि पैदल पोथना सम्म फेरी मत्थर उकालो लागेका हामी लो क्याम्पको ३०५० मिटरको उकालीमा पुग्दा पृथ्वीको गुरुत्वकार्षण भर्सेस पिडुलको शक्तिको राम्रै मापन भयो । व्यवस्थापनमा धेरै जसो कार्य प्रक्षेपणको आधारमा गरिन्छ । प्रक्षेपण सामान्यतया लिनियर गरिन्छ, अर्थात् निश्चित अनुपातमा बृद्धि वा कम हुने भन्ने अनुमान गरिन्छ । यदि पोखरा देखि पोथना सम्मको लगभग १५ डिग्रिको उचाईलाई प्रक्षेपण गर्ने हो भने तेस्रो दिन पुगिने बेस क्याम्प को ४५०० मिटरको उचाँइमा जम्मा लो क्याम्पको उचाईको अनुमानित लक्ष्य हुन्छ । यसले दुई दिनको अनुमान चुक (Projection Error) हुन जाने देखिन्छ । तर तात्पर्य प्रक्षेपणहरु काम नै लाग्दैनन् भन्ने होइन, सो मोटामोटी अन्दाजका लागि उपयुक्त हुन सक्छ र सम्पूर्ण जानकारी सहित गरिएको प्रक्षेपणमा चुकको सम्भावना कम हुन्छ ।
उकाली गाह्रो ओराली सजिलो हुन्छ: मेरो जन्मथलो नभए पनि सम्पूर्ण थकालीहरुको जस्तै पुखयौली मुस्ताङ्ग । अहिले जस्तो सहज बाटो नहुँदा घोडाको प्रयोग बेसी हुन्थ्यो । घोडाको उकाली चढ्ने क्षमता पनि मान्छेको जस्तै असंगती हुन्छ । मुल्य त्यसै अनुसार फरक पथ्र्यो । उकालीमा सुस्ताउने घोडालाई “ल्ह्न्च्या” अर्थात अल्छी भनिन्छ । उकालीमा सजिलो गरि बोक्नेलाई “ल्ह्म्बु” अर्थात लिडर वा नेता भनिन्छ । पोथना देखि माथि लाग्दा सबैको रफ्तारमा भिन्नता देखियो । जव उकाली आयो अनि बल्ल सबैको स्टामिना तथा कोलेस्ट्रोल लेभल विना रक्तपातको पक्का जाँच भयो । यसले सम्झनामा ल्यायो, समथरमा त सबै हिड्छन्, उकालीमा कुदेको पो पौरखी । ठ्याक्कै त्यही कुरा व्यवस्थापनमा लागू हुन्छ, रिसाइलेन्सनै पक्का लिडरको हुनु पर्ने मुख्य गुण हो । सहज अवस्थामा नेतृत्वको जाँच हुदैन, अप्ठ्यारो परिस्थितीमा संस्थालाई कसरी परिचालित गर्न सकिन्छ सो ले नै लिडरसिप प्रमाणित हुन्छ ।
नपहिल्याएको बाटो: उकाली चढ्दा विशेषत दुई वटा बाटा हुन्छन् । एउटा सहज तेर्सो बाटो हुन्छ, उकालो बिस्तारी जाने तर लामो । यो बाटो सजिलो पहिचान हुन्छ । अर्को बाटो त्यति पहिल्याउन सहज हुदैन तर बाटोसँग परिचित स्थानियहरुले प्रयोग गर्छन्, त्यो बाटोमा भिड हुदैन, चाडो चढ्न सकिन्छ तथा अलि असहज हुन्छ । सबैले हिडेको बाटोले जित्न सकिन्न, उकालीको जस्तै एकल बाटोमा अरुलाई उछिन्न सकिन्न । व्यवस्थापनमा “जिग ज्याग” सिद्धान्त भन्ने हुन्छ । अरु यो कुनामा हुँदा हामी सो भन्दा अगाडी अर्को कुनामा हुन सक्नु पर्छ । अरुले जे गर्यो त्यही गरेर विजयी हुन सकिन्न । नव बाटोहरु पहिल्याई सोमा हिड्न सक्नु नै सफल लिडरको अर्को आवश्यक गुण हो । मर्दीको उकालीमा सम्झेको अर्को सुत्र यो पनि हो ।
सन्घर्ष अनन्त यात्रा हो: पोथनामा चिया खान बस्दानै मेरी जिवनसाथी बिसाउने चौतारी खोज्न थालीसकेकी थिईन । त्यसपछिको लो क्याम्पसम्मको यात्राको उकाली हामी नहिड्नेलाई सगरमाथा चढे जस्तै भयो । एक हातमा रहेको लठ्ठी तथा अर्को छाती सम्म उठेको खुट्टाको साहारामा निरन्तर यात्रा गरियो । उकालो चढ्दा आँखाले देखुन्जेलको चोसो नै अन्तिम टुप्पो जस्तो लाग्ने तर त्यो आशा निमेश भरलाई हुने, अलि अघि पुगेसी फेरी थप उकाली देखिने । खुईय खुईय गर्दा गर्दै करिव चार बजे मा बल्ल लो क्याम्प पुगियो । मोवाईलको नेटवर्क आउने जाने थियो । बिहान लो क्याम्पबाट हिड्दा एक टाकुरो नेटवर्क देखियो । भाई राजु जसले केही अघि त्यही उकाली नापी सकेका थिए उनलाई फोन थिचे । लो क्याम्प पछि त सम्म सम्म छ सर, एकछिन एकछिन हो, धाडस दिए उनले । के को हुनु एकछिन सम्म आए जस्तो फेरी उकाली, मन मनै गाली गरे, मोरा । हाई क्याम्पमा पुगेसी यसो बिसाएर हेरे । माथि बेस क्याम्प तिर मान्छे हिडिरहेका थिए । त्यस भन्दा पनि माथि मर्दि हिमाल हासी रहेकी थिईन । अंग्रजीमा त्यसैले भनिन्छ, दिस इज नट दि एण्ड बट जस्ट ए टर्न । संघर्ष त्यस्तै नै हो । अनन्त अनि निरन्तर । भरखर क्यारियर गरेकाले बुझ्नु पर्छ, धैर्यता भन्दा अर्को ठूलो सुत्र छैन सफलताको ।
परिस्थितीजन्य समायोजन: व्यवस्थापनको अर्को महत्वपूर्ण कुरा हो जस्तो सुकै अवस्थामा घुलमिल हुन सक्नु । सम्भवत बिहान व्युझिंदा सबै भन्दा अगाडी स्वाभाविक रुपमा मोवाइलमा हात जान्छ मेरो, अटोमेटेड रुपमा । बेलुकी सुत्दासम्म पनि मोबाइललाई नै अन्तिम गुडनाईट गरिन्छ । तर यो यात्रामा सो मोबाइल राती लघुशंका जादा टर्च बाल्ने बाहेक काम भएन । आक्कल झुक्कल नेटवर्क आउदा बाहेक अन्य बेला फोन लागेन । सोलारले चार्ज भाको होटलको व्याटरी व्याकअप खाना खुवाउदा चैट भई सकेको थियो । अध्यारोमा छाम्दै खाट पहिल्याउनु बाहेकको बिकल्प थिएन । हाई क्याम्पमा रेष्टुरेन्टमा पोस्टर थियो, मोबाइल चार्ज गरेको २०० रुपैया मात्र । मानिस जस्तो अनुकुलन गर्न सक्ने जीव अन्य छैन । ए यस्तो भए बर्वादै हुन्छ भनी सोच्नु मिथ्या हो । समय र परिस्थितीसँग आवश्यकता सापेक्ष छ, निरपेक्ष छैन । जे चिज हामी अपरिहार्य भन्छौ त्यो नभए पनि फरक पर्दैन । त्यसैले जस्तो पर्छ त्यस्तै तर्छ भन्छन् । वातावरणसँग जती चाँडो घुलमिल हुन सक्यो, त्यती नै अस्तित्व बचाउन र आफ्नो कार्यमा रमाउन सकिन्छ ।
हाई क्याम्प पुगेर होटलमा भारी बिसाए पछि मलिलो लागेको घाममा एक क्यान वियर लिएर नजिकको ढिस्कोबाट ढुंगा फाल्दा लाग्ला जस्तो दुरिको हिमाललाई निहारे । दुई पलमै मिठो निन्द्रामा परेछु, बिना एसीको बातानुकुलित चिसो सिरेटोमै । हिड्ने यहीसम्म हो, काम फत्ते भयो भन्ने महशुस भएर हो वा त्यती धेरै हिडेर मेहनतको फल मिठो हुन्छ भन्ने उखान चरितार्थ भएर हो । काम नगर्ने खाली खोइरो खन्ने प्रबृत्तिकाले बुझ्नु पर्ने अन्तिम चुरो कुरो ।
(क्लीकमाण्डु डट कम मा मिति २०१९ फेब्रुवरी ७ मा प्रकाशित)

A Brief Insight into the Reckless Public Transport System in Kathmandu: Understanding it with Operant Conditioning Theory.
It is quite easy and comfortable for a bus ride in London. However it would be an unimaginable moment for a westerner or person from developed countries if they get into or even get near to a public vehicle in Kathmandu. Recently a public bus in Kathmandu ran into a shop and killed people inside because it was speeding too fast while trying to overtake a bus on the same route. It’s quite common scene that the bus goes to opposite lane just to get past the other vehicles faster, many times hitting vehicles coming from other direction or person walking on walking lane of opposite side. “Reckless Driving including speeding, swerving, sudden braking and accelerating are quite common in Kathmandu”2. Over 70% person in a recent study on “Gender and Public Transport in Nepal” conducted by The World Bank stated that the public transport were overcrowded1. In a micro bus which is common means of Public Transport with maximum capacity of 14 seats, there are 28 people at a time, where the driver stops for more than 10 minutes on average at every stop just to put more people even if there is no place to put your feet.8,9 Road safety is a major issue and everyday there are over 130 serious traffic accidents (over 1000 minor accidents) reported in Kathmandu1 alone which is quite high in a city of 300 Square Miles with only 5,300 public transport vehicles including buses, micro buses, mini buses, tempos and taxis plying. The rise in the motorbikes (568,845 in total) out of total of 718,135 vehicles in the city3 is the proof that people commuting in the city are preferring private vehicles over the public ones due to the recklessness.3
What could be the behavioral causes that allow such actions of the drivers in two places contrast so highly and what make them behave so differently? The Operant Conditioning Theory could explain how the reckless behavior in the public transport drivers in Kathmandu developed. Learning is acquiring new knowledge and applying it for the future. 4 It can either be associative or observational. The associative learning is basically explained by two theories namely Classical Conditioning and Operant Conditioning. Operant Conditioning or instrumental conditioning is a type of learning in which an individual’s behavior is modified by its antecedents and consequences 6. Human being tend to build association between behavior and the consequences of the behavior. For example if a child is given a dessert that she likes every time she finishes her dinner well, it is more likely that she finishes her dinner well in subsequent days. So basically a behavior is reinforced by the rewards or punishments. The rewards or punishments can either be positive or negative. In positive the rewards or punishments are present or given while in negative the rewards or punishments are absent or removed.
There is no fixed timing system of public vehicles in Kathmandu. The public transport though starts in fixed intervals, it is not regulated or monitored in between as to how much it spends in a station or at what speed it is going. Also no system is in place to monitor whether the vehicle is overcrowded or not. The vehicle is owned by private owner who gives it to the driver for operating. Though the driver is in fixed salary, there is no way of checking how many passengers got into the vehicle in a day. So basically the driver gives a tentative amount that is expected by the owner in fixed scale every day and pockets the rest of the income. So every day the more no. of overcrowded passengers that the driver is able to put into the vehicle, the more he can pocket the income on top of his fixed salary. Since there is no positive punishments from regulatory bodies, but instead only the positive rewards in return to his work, the driver is more and more conditioned to follow the same routine of overcrowding the vehicle with more no. of passengers. His behavior is reinforced with the positive consequences as well as lack of negative consequences.
The reckless driving is understandable and explainable in the same manner. Suppose a bus leaves the starting point every 5 minutes. Though the second bus starts after 5 minutes, it tries to overtake the first bus so that it can pick up the passengers in next station. If they are able to pick up the passenger in the next station, there is reward of extra income to them, hence the positive reinforcements to that behavior. Since this goes on unpunished, there is more encouragement to the behavior.
The theory further states that if the schedule of reinforcements are in variable ratio, the response is more intense. In overtaking the bus in front, there is variable probability that the reward of additional passenger would be available, hence this explains the high intensity of the reckless driving to the extent that they could run into a shop to kill people.
The remedy to this behavior could be that the reward for the reckless behavior be removed. This can be done by putting electronic card system (like the Oyster Card in London) where there is no use of cash. If there is no cash, but electronic points, it cannot be pocketed. Thus because the overtaking of the vehicle is front would not be rewarded or reinforced by the reward this will discourage the reckless driving. The electronically collected money would be cashed in a bank account of the owner of the vehicle. The drivers can be compensated with higher salary so that they don’t oppose this idea but the salary has to be fixed so that the very motivation of putting more passenger is taken away. We can be sure that with this system, it will be the driver who would ask the passenger to get off the bus if there is overcrowd over the capacity of the bus, just as it happens in London.
(Submitted for course fulfillment to London School of Economics on Consumer Behaviour)
References
1 The World Bank Group. “Gender and Public Transport, Kathmandu, Nepal.” Study Report. 2013.
2 Udas, Suman. “Public Transport Quality Survey”, Study Report for Clean Air Network Nepal. 2012.
3Department of Transport Management of Nepal. Website http://dotm.gov.np/
4 Kardes, Cline and Cronley, “Consumer Behavior, Science and Practice”. Ceengage Learning. 2010
5 Hoyer, Maclnnis, Pieters. “Consumer Behavior”, 6th Edition. Ceengage Learning, 2014
6 http://en.wikipedia.org/wiki/Operant_conditioning
7 http://psychology.about.com/od/behavioralpsychology/a/introopcond.htm
8 http://dineshmurmurs.blogspot.co.uk/2008/09/micro-woes.html

Benford’s Law: An Analytical Tool For Sniffing Frauds
As a High School Student I was always fond of asking questions to “Guru Joe” an online game character on the web, portraying as a fortune teller. For every funny questions I asked, he would look thoughtful, see through his magic ball and show me either thumbs up or down. Now as a professional accountancy student I along with my colleagues come through many difficult situations where we need to assess whether there are any anomalies, frauds, unusual transactions, misleading information etc. in the propositions put before us. But this time perhaps we need not depend on “Guru Joe” or in fact his programmer for any doubts, thanks to the analytical tools and techniques that have been developed over years. One of such analytical tools is Benford’s Law, a digital analysis tool also known as the first digit law or the first digit phenomenon or leading digit phenomenon that evaluates the digital frequencies over the position of appearance in the data provided to detect anomalies.
Benford’s Law
Benford’s Law suggests that when considerably large population of naturally calculated unbiased random numbers is selected their digits tend to follow a fascinating phenomenon। We know that there are 9 natural numbers viz। 1 to 9, thus with our simple probability the odds or chances that the first digit of any no. being 1 should be 1/9. However this might not be true, because if we empirically observe any large population of data, we find that the percentage of the first digit being 1 is around 30.10 %, 2 is 17.61% and so on in decreasing order. To our amusement, this trend is unconditionally followed by every group of numbers equally truly like the Law of Gravity, provided that the numbers are not biased or manipulated.
This was exactly what Simon Newcomb, an American Astronomer and Mathematician noticed way back in 1881 when he observed that the library copies of the books of logarithms were more worn out in the beginning pages which dealt with low digits and progressively less worn on the pages dealing with higher digits। He inferred from this pattern that the fellow scientists used those tables to look up numbers which started with numerical one more often than those starting with 2, 3 and so on. He thus calculated that the probability that a number has particular non-zero first digit is given by:
P(D1=d1) = log10(1 + 1/d1) for d1 {1, 2,...,9}
So probability of first digit being 9 would be log10 (1 + 1/9) i.e. log10 (1.11) or 0.04576. This means that the probability of first digit being 9 is 4.576%.
Though Newcomb formulated the model he never gave the theoretical explanation to the phenomena neither he extensively tested his theory। It was only in 1938 almost 50 years later that Dr. Frank Benford, a physicist working in General Electric again noticed that the first few pages of his logarithmic table was more worn out than last few. He made an extensive test of his hypothesis by collecting 20 lists of numbers with a total of 20229 observations. His lists came from varied sources, such as geographic, scientific and demographic data. One list contained all the numbers in an issue of Reader's Digest. He found that about 31% of the numbers had 1 as the first digit, 19% had 2, and only 5% had 9 as a first digit. Benford then made some physics-related assumptions about the distribution of naturally occurring data and, using integral calculus, he computed the expected frequencies of the digits and digit combinations (see Table 1 for the calculated expected frequencies of the digits).

The above table suggests that the probability of appearing 1 in the first place is 30।10 % whereas in second place is 11।39 %। Similarly the digit 6 should appear 6.69 % in first place of the numbers under consideration.
With appropriate variations in the formula the numbers provided can be tested in various levels of tests, wherein the digits’ appearances can be tested at various positions and even for various combinations like first two digits, last two digits, second digit, last digit etc।
Logical Explanation of Law
A billion rupees worth question would be why the digits appear in exactly the calculated frequency.
An intuitive explanation of Benford's law is to consider the total assets of a mutual fund that is growing at 10% per year। When the total assets are Rs. 100 million, the first digit of total assets is 1. The first digit will continue to be 1 until total assets reach Rs. 200 million. This will require a 100% increase (from 100 to 200), which, at a growth rate of 10% per year, will take about 7.3 years (with compounding). At Rs. 500 million the first digit will be 5. Growing at 10% per year, the total assets will rise from Rs. 500 million to Rs. 600 million in about 1.9 years, significantly less time than assets took to grow from Rs. 100 million to Rs. 200 million. At Rs. 900 million, the first digit will be 9 until total assets reach Rs. 1 billion, or about 1.1 years at 10%. Once total assets are Rs. 1 billion the first digit will again be 1, until total assets again grow by another 100%. Table 2 and 3 explains the dominance of lower digits in the first place of the numbers.


The persistence of a 1 as a first digit will occur with any phenomenon that has a constant (or even an erratic) growth rate। The numbers are “base invariant” and “scale invariant” as well thus it won’t matter whether the numbers are in any currency, is multiplied by something or divided by something, it will unquestionably follow the law।
Applicability in the Accounting and Auditing Profession
While the applicability of the Benford’s law is wide-ranging, its application to the accounting and auditing profession has been a boon। It helps to find out fraudulent and irregular perpetrated accounts and data prepared with mala-fide intention. Benford’s law actually has been integral part of detecting tax frauds and bank frauds and is included in the analytical procedures by many big firms and government authorities. The application could range from simple application through spreadsheets to the specialized computer programs with complex calculations.
So how can it be used to detect fraud would be the question। To explain it, let’s discuss an incidence in Georgia Institute of Technology. Dr. Theodore P. Hill from the University asks his mathematics students to go home and either flip a coin 200 times and record the results, or merely pretend to flip a coin and fake 200 results. The following day he runs his eye over the homework data, and to the students' amazement, he easily fingers nearly all those who faked their tosses. When interviewed Dr. Hill told that the reason he was able to point out the fake data was because many students didn’t actually know the real odds of such an exercise and thus they couldn’t fake data convincingly. Actually when the coins are tossed for a long period of time, at some point the heads or tails tend to appear for more than 6 consecutive times in a row. The student who pretended to flip the coin couldn’t guess this phenomenon and easily got caught.
Same is the problem with the fraud perpetrators। People cannot behave truly randomly even when it is to their advantage to do so and try to impose their intelligence while faking accounts। Even when people invent numbers without a goal such as fraud in mind, the digital frequencies do not conform well to Benford's Law.
So by extracting the percentage of actual appearance and then comparing it with the calculated percentage of Benford’s Law will give us an idea whether there are any abnormalities। If there seem vast deviations in the appearance of digits from calculated frequency, it can be reasonably assumed that there is something wrong.
One such instance where the auditors were able to point out fraud was in a bank where the digit 4 appeared quite abundantly than the Benford’s law suggested in credit card debt write-off figures। While making further scrutiny auditors found that the officer writing off most of the debts had the credit write off limit of $ 50,000. So what he was doing was actually calling on his friends to use credit card for purchases exactly just below 50,000 and not pay. And then he would write it off. Thus figure four was appearing more than it should have been.
Many countries have also implemented the use of Benford’s law to find out tax fraud where the tax returns data submitted by tax filers are scrutinized through specialized software। Several States of US including California are using detection software based on Benford's Law.
When to use and when not to use the Law?
It is however to be taken care that the fit of number sets with the Benford’s Law can also be fallible। There is need of applying the law with reasonable discrimination. Suppose if we check the telephone numbers of the Kathmandu Valley obviously we would find that the frequency of appearance of digit 4 will be almost cent percent. Similarly when there is fixed sales value like Rs. 24 per unit of sale unit, obviously we would find that digit 2 will appear more frequently than others if there is abundance of single unit sales. Thus care should be taken not to jump on the assumption of fraud as soon as the deviations are found. Biased numbers, assigned numbers like the Cheque no. or Invoice no. and the numbers just picked up without going through any calculations or arithmetic do not tend to follow the law. Dr. Nigrini a prominent researcher in the application of Benford’s Law in Accounting further explains "You can't use it to improve your chances in a lottery. In a lottery someone simply pulls a series of balls out of a jar, or something like that. The balls are not really numbers; they are labeled with numbers, but they could just as easily be labeled with the names of animals. The numbers they represent are uniformly distributed, every number has an equal chance, and Benford's Law does not apply to uniform distributions."
The law can be reasonably used to test most sets of accounting data including accounts receivables, accounts payables, disbursements, sales, expenses, full year’s transactions, bank transactions or any transaction level data। However it won’t be working to the numbers that are influenced by human thoughts like prices of Rs. 1.99 etc.
An example of digital analysis
Still skeptical of the real applicability of the law even after going through lots of texts over the internet on this particular topic I decided to test it myself। So I opened up an Excel Sheet and entered into it first 518 numbers appearing in the Mid January 2004 Bank and Financial Statistics published by Nepal Rastra Bank available to me. To my astonishment, the results were nearly identical to the Law. Table 4 and Graph 1 depict the result obtained.


The digits’ frequency nearly followed the law with only the significant variance being in the appearance of digit 2 of 3।43% and digit 7 of 2.32%
Easy Steps to Perform Test in Excel
If you still have any doubt about the law, the following easy steps to perform First Digit Benford Test in Excel could help you out।
§ Open up an Excel Spreadsheet and fill in the first column “A” with available numbers from any source (for distinctive appliance of Law large population is required usually more than 50 numbers).
§ In the second column “B” extract the first digit of the numbers entered with the formula
= LEFT (cell no, 1)
§ Enter numbers 1 to 9 in the third column “C”.
§ In fourth column “D” find out the frequencies of the appearance of the digits in Column B with COUNTIF function. For instance against digit 1 in cell D1 enter the formula.
= COUNTIF (cell range in Column B, 1)
Similarly for counting number of appearances of digit 2 enter the following formula in Cell D2
= COUNTIF (cell range in Column B, 2) and so on till digit 9.
§ After finding the required frequencies of all digit through 1 to 9, total the numbers in cell D10 by formula
= SUM (D1:D9)
§ In column “E” find the percentage of appearance of each digit by dividing the no of appearance of each digit by the total in cell D10 and multiplying by 100.
§ Enter the Benford’s suggested % in column “F” as given above in Table 1.
§ Deviations from the Law can be calculated by subtracting actual appearance % in cell E from Benford’s suggested % in column “F”.
Conclusion and Further Reference
The sustainability and value of any profession undoubtedly depends on the quality of services the members in the profession provide. Unlike to sticking to conventional judgemental techniques in performance of audit and other related services new developments and tools shall be embraced for the value addition in the services provided. Perhaps applying various digital and computerized analytical tools like Benford’s Law Test would be one step towards it.
Benford’s Law seems to have vast scope of appliance in sniffing corporate fraudulent reporting and anomalies to finding the tax frauds being a handy tool to our profession. Its usefulness is pervasive in basically pointing suspicion at frauds, embezzlers, tax evaders, sloppy accountants and even computer bugs.
(Published in ICAN Journal)
Further References
§ I’ve Got Your Number, Mark J. Nigrini
§ http://www.nigrini.com/
§ Following Benford’s Law or Looking Out for No. 1, Malcolm W. Browne
§ The First Digit Problem, R. Raimi
Who Am I?
The famous adage goes “No one steps on the same river twice”. We change with every tick of our watch, every moment we are a new one. Not to forget as well, whatever we are now has come through smoothing against the friction of time. Time gives happiness, time gives pain and again time heals, in process teaching us something. So everything is all about learning, and in essence life is also about learning. As a child we started to babble few words, as a toddler we started to totter, as an adolescent we began to recognize letters, as a teenager we began to be attracted to opposite sex and as a youngster we started worrying about our career. Perhaps time will come when we will start thinking about our children and then their career, their marriage so and so on. So the learning process keeps going on till the extreme end of life, then we would be trying to search a peaceful place to rest our soul.
Learning for me seems to be seeing, listening, feeling, experimenting and finally deciding whether it’s right or not for me. The surrounding environment, my family, my friends and foes, my bosses, my teacher, my colleagues, my classmates, the society I belong to, the school I attended, the books I studied, the places I visited, the god I worship every body has certainly contributed in my learning. Whatever I am today is not only myself, but sum of whatever I have experienced, seen, heard and learnt put together.
So as I sit down to count today, I feel that everybody in my life taught me something. People that I meet inside Micro-Buses, those who pass by me as I walk, those who stare me, those who smile at me, everybody is giving me a lesson. Nowadays I try to find best things from the worst people I meet. I find that everybody, I shall repeat everybody, have something special, that no other has.
This doesn’t mean that whatever I have seen was always inspiring. Once I saw a selfish guy brings around 70 years old helpless woman in a tempo and leave in the midst of Sohrakhutte. Annoyed after knowing from her that the person bringing her was his own son, people gathered around brought everything they could to offer. Everyday I would get down from my micro-bus automatically go to the banana vendor, buy a bunch and offer in her shivering hand. That was all I could offer as a student, and her tearful penetrating eyes taught me what compassion means.
So that’s what I have learned, I am little bit of everybody and everything put together. We should try to see the best part of everybody and everything. That way round perhaps we will forget their darker side, only then would they appreciate us and forgiveness prevail. Only then would real peace come.

Micro Woes
Many friends of mine compare my bike wid a horse, and I have no option other than to accept it coz its mileage is such that it eats like what horse eats gram. However its not the cause I don't prefer riding bike, its no more same passion when I used to ride my uncle's or brother's bike without asking them (the workshop ppl taught me how to direct the line and start without key). Unless extremely needed, I give complete rest to my metal giant.

Cock-a-doodle-do
I recently went through a forum, people were discussing how a donkey make sounds (wat a useless topic). Here's wat one logically explained.
step 1: the donkey breaths in : that makes an "ah" sound
step 2: it breaths out: that makes an "i" sound. So it is "a-i" "a-i" "a-i" (don't try to make that sound, Nepal too has got copyright act).
More stupid must be me, who read it through (top till bottom). I'm thinking of running one other topic, how does a cock cock-a-doddle-do (thats what i suppose must be a cock's sound called). Or may be wats the difference between the sounds of cock's in ktm and pkr. I usually din't get a chance to hear cock's sound, except when dad bought it to make spicy curry(for ur info I'm a veg now). People here in Kathmandu seem to crazily raise cocks, may be side income in this city filled with poor (or may be food for the cats).
Actually cock's issue din't popped up without reason, I'm hearing it quite often nowadays as I am playing owl these days bitten by my exam bug. Surprising though is that, cocks here begin their riyaz quite early as 1. Few crazy cocks even made sounds at 12. Is that becoz of the light of my havel's energy saving bulb that they confuse its morning (quite a topic for a new research or advertisement of havel's light, rimponche). More astonishment to me is that they suddenly stop it around 2.30 and again start it at around 5, so I guess they are making two sessions, one for people like me whose morning starts at midnight and the other for usual ones.
Our gatekeeper has also got two cocks, one small one big. Its quite a fun to scare them and run after to make them half fly in air to escape. Its just so funny that it gets alert as soon as I am around, just like an armyman aware of its enemy. Anyway it doesn't know that I am a veg else it must be less scared, don't dare to tell it.
Leave the cocks, I need to get back to my elearning site. So Long till next time..........
